07. Partial Plans

Partial Plans Explained

Figuring out how many partial plans are possible given a particular search space can be confusing. Here we'll step through the logic of how you can arrive at an answer for the example above.

Given that you can't move off the grid, and you can't move diagonally, from the start location you have three options, up, down or right like this:

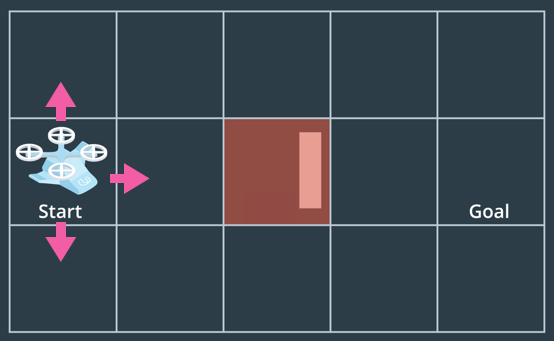
Each of these moves represents a unique partial plan. You could think of keeping track of the moves in each partial plan in lists like this:

plan1 = ['Start', 'up']
plan2 = ['Start', 'right']
plan3 = ['Start', 'down']

You can visualize each of these partial plans as now including specific cells in the grid like this:

All plans include the starting cell and each includes one other cell as well at this point, the one above Start for plan1 (in green), to the right of Start for plan2 (in red) and down from Start for plan3 (in blue).

Now comes the choice of how to expand each of these plans. Given the rules of the game, you can see that you have one option with plan1, which is to move right. You have two options with plan2, which are to move up or down (can't move into the obstacle cell) and one option to move right from plan3 as well.

At this point, it doesn't matter which plan you expand first, so let's just go ahead and start by expanding plan1 in the only way possible, which is to move right like this:

Now plan1 has been expanded to include a move to the right. What happens now if you try to expand plan2? Given that the cell above plan2 is already occupied by plan1, and separate plans can't merge together, there is only one remaining option for expanding plan2, which is to move down like this:

Now your collection of partial plans looks like this:

plan1 = ['Start', 'up', 'right']
plan2 = ['Start', 'right', 'down']
plan3 = ['Start', 'down']

What then becomes of plan3? At this point, the only direction (right) that plan3 had as an option to expand in is already occupied by plan2! This is not a problem for your search algorithm, it just means that there is nowhere else for plan3 to go. It's still a valid partial plan, but it's basically a dead plan because it can no longer be expanded.

plan1 and plan2 can continue marching happily toward the right for a couple moves like this:

But now the landscape has changed! Both plan1 and plan2 have two options for directions to expand in. This means there is an opportunity for branching and forming a new partial plan. Suppose you first expand plan1 to the right. You could then add a new partial plan branching off of plan1 going down. Let's call that plan4. While we're at it let's also expand plan2 one more step to the right:

Now, you have four plans in total and you've explored all cells in the grid. Any of these plans could be expanded to reach the goal and all of them represent valid paths that your vehicle could travel from start to goal.

You may have noticed, however, that there wasn't much rhyme or reason here in deciding which plan to expand next and in which direction. You can imagine a scenario where either plan1 or plan2 was left for dead instead of plan3.

In the case that you expand plan2 up and down before expanding plan1 or plan3, you'll end up with 5 total plans that look like this (plan5 could just as well take path above the obstacle):

The truth is that there are many different strategies to consider when deciding how to expand your partial plans, and that's what we'll look at next!